Implementing Sum of Subset by Backtracking in Java

The subset sum problem is a classic problem in computer science and is often solved using backtracking. The goal is to find subsets of elements selected from a given set whose sum adds up to a given number K.

Understanding the Problem

Given a set of n positive integers and a value m, the task is to determine all possible subsets whose sum is equal to m. This problem can be efficiently solved using backtracking.

Approach: Backtracking

Backtracking is a general algorithmic technique that incrementally builds candidates to a solution and abandons a candidate as soon as it is determined that the candidate cannot lead to a valid solution. In the subset sum problem, we:

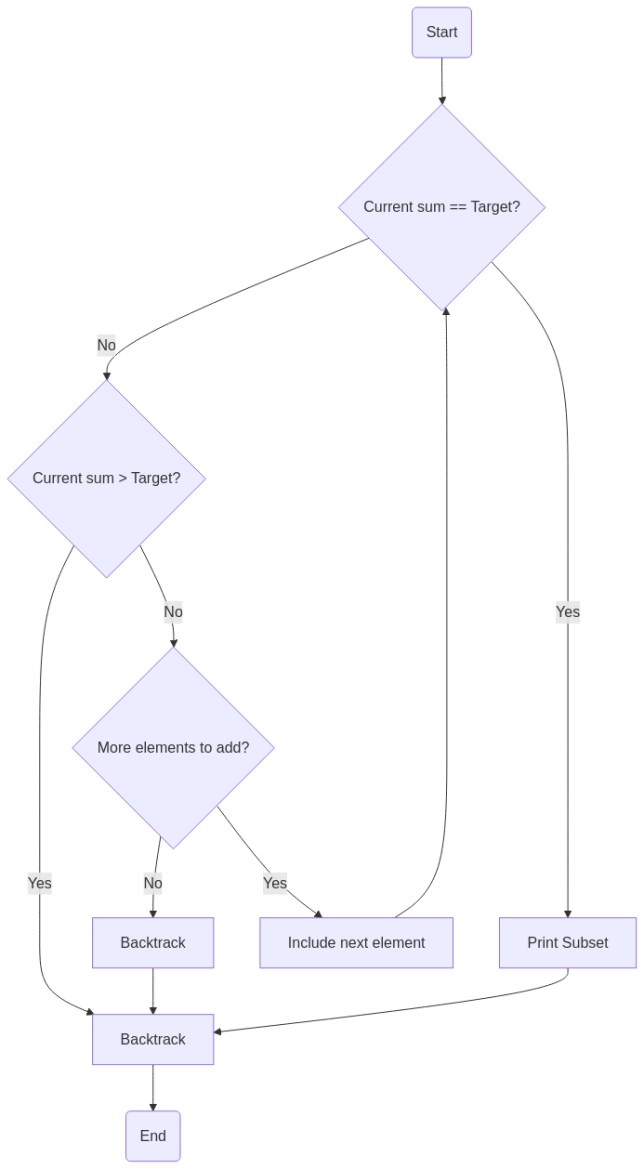
Start with an empty subset.
Add elements one by one while keeping track of the sum.
If the sum equals m, print the subset.
If the sum exceeds m, backtrack and try another possibility.

Flowchart

Java Implementation

The following Java program implements the sum of subset problem using backtracking:

import java.io.*;
import java.util.*;

// Class to implement Sum of Subsets problem
class SubsetSum {
    int targetSum; // Target sum to be found
    int[] setElements; // Array to store set elements
    int[] included; // Array to track included elements in subset

    // Constructor to initialize arrays
    public SubsetSum(int n) {
        setElements = new int[n];
        included = new int[n];
    }

    // Recursive function to find subsets whose sum equals targetSum
    public void findSubsets(int currentSum, int index, int remainingSum) {
        included[index] = 1; // Include the current element
        
        // If a valid subset is found, print it
        if (currentSum + setElements[index] == targetSum) {
            printSubset(index);
        } else if ((currentSum + setElements[index] + setElements[index + 1]) <= targetSum) {
            // Recur to include the next element if it does not exceed target sum
            findSubsets(currentSum + setElements[index], index + 1, remainingSum - setElements[index]);
        }
        
        // Backtrack: Exclude the current element and check next possibility
        if ((currentSum + remainingSum - setElements[index] >= targetSum) && (currentSum + setElements[index + 1] <= targetSum)) {
            included[index] = 0;
            findSubsets(currentSum, index + 1, remainingSum - setElements[index]);
        }
    }

    // Function to print the subset that meets the target sum
    private void printSubset(int index) {
        System.out.print("Subset found: ");
        for (int i = 0; i <= index; i++) {
            if (included[i] == 1) {
                System.out.print(setElements[i] + " ");
            }
        }
        System.out.println();
    }
}

// Driver class to take input and execute the program
class SubsetSumDemo {
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        
        System.out.print("Enter the number of elements in the set: ");
        int n = Integer.parseInt(reader.readLine());
        
        SubsetSum subsetSumSolver = new SubsetSum(n);
        int totalSum = 0;

        System.out.println("Enter the elements of the set:");
        for (int i = 0; i < n; i++) {
            subsetSumSolver.setElements[i] = Integer.parseInt(reader.readLine());
            totalSum += subsetSumSolver.setElements[i];
        }

        System.out.print("Enter the sum to be computed: ");
        subsetSumSolver.targetSum = Integer.parseInt(reader.readLine());
        
        System.out.println("Subsets whose sum is " + subsetSumSolver.targetSum + " are:");
        subsetSumSolver.findSubsets(0, 0, totalSum);
    }
}

Explanation of Code

Class SubsetSum:
- Defines an array setElements[] to store input set elements.
- Uses included[] to indicate whether an element is included in a subset.
- Implements the backtracking function findSubsets().
Backtracking Function findSubsets(currentSum, index, remainingSum):
- Adds elements to a subset and checks if their sum matches targetSum.
- If the sum is reached, the subset is printed.
- If adding the next element does not exceed targetSum, it recurs further.
- If no valid subset is found, it backtracks.
Class SubsetSumDemo:
- Takes user input for the set and target sum.
- Calls findSubsets() to compute and display subsets that sum to targetSum.

Sample Input/Output

Enter the number of elements in the set: 4
Enter the elements: 
11 13 24 7
Enter the sum to be computed: 31 
Subsets whose sum is 31 are:
Subset found: 24 7

Time Complexity Analysis

The time complexity of this solution is O(2^n) in the worst case, as we are considering all subsets.
Pruning through backtracking helps eliminate unnecessary recursive calls, making it more efficient than a brute-force approach.

The sum of subset problem is an excellent example of how backtracking can be used to efficiently solve combinatorial problems. The given Java implementation demonstrates an elegant way to find subsets whose sum equals a given target. This method is particularly useful in optimization problems and decision-making algorithms.

@ankurm